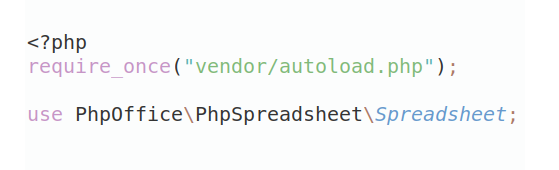
Download the PHP package mgrechanik/ant-colony-optimization without Composer

On this page you can find all versions of the php package mgrechanik/ant-colony-optimization. It is possible to download/install these versions without Composer. Possible dependencies are resolved automatically.

FAQ

After the download, you have to make one include require_once('vendor/autoload.php');. After that you have to import the classes with use statements.

Example:
If you use only one package a project is not needed. But if you use more then one package, without a project it is not possible to import the classes with use statements.

In general, it is recommended to use always a project to download your libraries. In an application normally there is more than one library needed.
Some PHP packages are not free to download and because of that hosted in private repositories. In this case some credentials are needed to access such packages. Please use the auth.json textarea to insert credentials, if a package is coming from a private repository. You can look here for more information.

  • Some hosting areas are not accessible by a terminal or SSH. Then it is not possible to use Composer.
  • To use Composer is sometimes complicated. Especially for beginners.
  • Composer needs much resources. Sometimes they are not available on a simple webspace.
  • If you are using private repositories you don't need to share your credentials. You can set up everything on our site and then you provide a simple download link to your team member.
  • Simplify your Composer build process. Use our own command line tool to download the vendor folder as binary. This makes your build process faster and you don't need to expose your credentials for private repositories.
Please rate this library. Is it a good library?

Informations about the package ant-colony-optimization

All versions of ant-colony-optimization with dependencies

PHP Build Version
Package Version
Requires php Version ^8.0
Composer command for our command line client (download client) This client runs in each environment. You don't need a specific PHP version etc. The first 20 API calls are free. Standard composer command

The package mgrechanik/ant-colony-optimization contains the following files

Loading the files please wait ....